向量检索算法HNSW
Hierarchical Navigable Small World (HNSW)是应用最广泛的近似最近邻检索算法之一,它基于小世界模型,采用类似跳表的分层索引机制,在保证查询效率的前提下,还能动态插入数据。HNSW 算法的原作者开源了一个参考实现hnswlib,本文将以此实现为基础对该算法进行讨论。
索引结构
下图是 HNSW 索引结构的示意图(这张图出自 HNSW 的论文1,在网上搜到的很多关于 HNSW 的资料都直接引用了这张图)。HNSW 索引是一个分层结构,每一层是一个邻近图(Proximity Graph),每个点有若干条无向边连接到它在该层内的近似最近邻。最底层(0 层)包括了所有数据点,从 1 层往上数据点的数量是指数递减的,第 i+1 层的点是从第 i 层随机选择的。最顶层只有一个点,作为查询的入口。
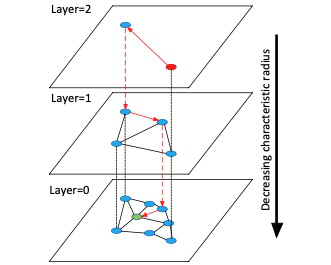
在创建索引时,通过参数 M 来指定每一层中数据点的最大邻居数。对于第 0 层,\(M_{max0} = 2 * M\),对于其他层,\(M_{max} = M\)。因此 M 越大,每个点占用的空间也就越大。
每个数据点投影到最大层数 \(l\),是根据指数衰减概率计算出来的,公式为:\(l = -\log(uniform(0 .. 1)) * M_L\) (公式1)。其中 \(uniform(0 .. 1)\) 为区间 [0, 1) 上的均匀分布,\(M_L\) 是正则化因子,它决定了数据点被投影到 1 层及以上的概率。作者在论文中给出建议取值是 \(M_L = \dfrac{1}{\log M}\)。因此 \(M\) 越大,\(M_L\)越小,数据点被投影到 1 层以上的概率也就越小。
我估算了一下,发现通常数据点被提升的概率是很小的。假设 \(M = 16\),那么 \(M_L \approx 1.2\),从 0 层提升到一层的概率大概是 6% 左右。因此HNSW索引层高的期望值并不高,1 层以上的数据量也比较小,主要的空间开销在 0 层。但是既然是随机的,那么如果 \(uniform(0 .. 1)\) 的值无限趋近于 0,\(l\) 就会趋近于无穷大,所以理论上还是有可能产生出一个非常高的层级。
综合以上 2 点,参数 M 直接决定了索引占用空间的大小。虽然 M 越大,数据点被提升到 1 层及以上的概率越小,但是每个点在 0 层占用的空间却更大,而后者才是索引的主要空间开销,因此可以近似的认为索引的空间占用跟 M 是成正比的。这里的索引空间只是存储 HNSW 图结构的空间,不包括向量数据本身。在实践中,向量数据本身占用的空间经常是远大于索引的。比如 128 维 float 类型的向量,大小为 1KB。M = 16 的情况下,索引 0 层占用的空间为 2 * 16 * 4 = 128 字节,要比向量本身小多了。
索引查询
在 HNSW 的分层结构中,第 1 到 maxLevel 层相当于为 0 层的全量数据建立了不同精度的缩略图,通过对这些缩略图的搜索,可以快速定位到 0 层中一个距离查询向量较近的点,从而缩小 0 层的搜索范围,达到提升查询效率的目的。
假设要查询向量 q 的 k 个最近邻居,HNSW 的搜索过程如下:
从顶层入口点 EP 自上向下搜索到 1 层,每层找到距离 q 最近的 1 个点作为下一层的入口。层内搜索采用贪婪算法,具体来说,算法从当前层的入口点开始,遍历它的所有邻居,并计算每个邻居和 q 的距离,找到距离最小的邻居,移动到该点,并重复以上的搜索过程。如果所邻居点到 q 的距离都要大于当前点,则算法终止,当前点就是本层中距离 q 最近的点,也是下一层搜索的入口。
在 0 层用贪婪算法查找距离 q 最近的 efSearch 个点。同样使用贪婪算法,搜索过程使用一个小顶堆 candidates 作为搜索候选队列,使用一个最大容量为 efSearch 的大顶堆 top_candidates 作为结果候选队列。具体搜索方法为:从上一步中得到的 0 层入口点开始,遍历它的所有邻居,计算它们和 q 的距离 d,如果 d 比当前 top_candidates 中的最大距离要小,或者 top_candidates 还没有达到最大容量,就把该邻居放入 top_candidates 和 candidates,否则就丢弃。遍历完当前点的邻居之后,再从 candidates 中取出下一个点进行遍历,如果 candidates 为空,则搜索终止,从 top_candidates 中选出距离 q 最近的 k 个点作为结果返回。由于 HNSW 使用的是无向图,遍历过程中会出现环路,需要记录下已经访问过的每个点,如果再次遇到就直接跳过。
索引构建
索引构建的过程就是向一个空的索引中逐个插入数据点的过程。插入数据点 q 的步骤如下:
按照公式 1 计算 q 最高投影的层数 l 。
从顶层入口点 EP 开始向下搜索到 l+1 层,每层找到 1 个距离 (q) 最近的点作为下一层的入口。方法跟查询步骤 1 相同。
从 l 层向下到 0 层,依次将 q 插入每一层,第 i 层插入过程如下:
a. 找到 q 在第 i 层的 \(M\_{max}(i)\) 个最近邻居,方法跟查询步骤 2 相同。
b. 建立 q 到这些邻居的边。
c. 对每个邻居点 n ,建立其到 q 的边。如果它的当前边数小于最大值 \(M_{max}(i)\) 则直接添加到 q 的边,否则就需要从 n 现有的邻居和 q 这 \(M_{max}(i)+1\) 个点中间选择 \(M_{max}(i)\) 个作为 n 的新邻居。这里的选择逻辑稍微有点绕,简单来说,就是按照到 q 的距离从小到大的顺序,逐个把所有候选点添加到 n 的邻接表,而每个添加的点 x 必须要满足如下条件:x 到 q 的距离要小于 x 到所有已经添加的点的距离。这个算法在原论文的第 3、4 节里都有说明,结合起来看更容易理解。不过,我暂时还没有理解为什么要用这种方式来选择。
删除和更新
HNSW 算法的一大优势,就是可以动态插入数据,因为索引的构建过程本身就是逐条插入数据的过程。但是删除就不那么直接了。删除一个点时,也要同时调整它在每一层的邻居点,以保证邻近图的结构和性质不变,否则查询效率会受到影响,极端情况下甚至有可能变成非连通图,导致某些点在查询中无法被访问到。调整邻居点的最简单的做法就是把每个邻居点重新插入一遍,但是这样效率就太低了。
hnswlib 中的实现是通过标记的方式进行逻辑删除。实现简单,效率也很高,但是有两个问题:一是逻辑删除并不会释放空间,二是会影响后续查询的效率。少量删除时问题不大,但是如果删除的数据多了,这两个问题就会比较严重。
对于更新问题,一种简单的方案是把它看做先删除旧向量,然后添加新向量两个操作。这种方式下还是会有前面删除的问题。hnswlib 采用了另一种方案,直接覆盖旧的向量值,并且从 0 层向上逐层修改图结构。修改的方法跟插入不太一样,并不会用贪婪算法去遍历查找新点的最近邻居,而从旧点的 2 度邻居里查找。另外,算法会按照一定概率随机选择旧点的邻居进行更新,通过调整概率的大小,可以在性能和准确性之间进行平衡。hnswlib 的实现比较简单,很多问题并没有考虑周全,在并发负载下,这里更新算法的实现还是有一些问题。
一些简单的测试
hnswlib 中自带了一个简单的 benchmark 工具 sift_1b.cpp,使用 sift_1b 测试数据集对索引的构建和查询性能进行测试。运行测试前需要先执行 download_bigann.py 脚本下载测试数据集,数据集比较大,压缩包由 90 多 G,解药后 120 多 GB。测试数据集为 128 维向量,每个分量是 1 字节整数,向量总数量 10 亿。另外包含了一些测试向量,每个测试向量都预先计算好的最近邻居,用于召回率测试。
测试平台为阿里云ecs.g6.4xlarge,16 核 64G 内存。
构建速度
sift_1b.cpp 中使用了 openmp,默认并行线程数 = cpu 核心数,所以 cpu 基本上是全部跑满的。
| 数据集大小 | 索引参数 | 构建耗时(s) | 平均速度(/s) |
|---|---|---|---|
| 10M | M = 16; efConstruct = 500 | 1327.72 | 7531 |
| 10M | M = 16; efConstruct = 100 | 323.895 | 30874 |
| 10M | M = 8; efConstruct = 100 | 214.525 | 46614 |
| 100M | M = 16; efConstruct = 40 | 1806.32 | 55361 |
内存占用
内存占用以测试结束时进程 RSS 为准。
| 数据集大小 | 索引参数 | 内存占用(MB) | 持久化文件大小(GB) |
|---|---|---|---|
| 10M | M = 16; efConstruct = 500 | 4067 | 2.6 |
| 10M | M = 16; efConstruct = 100 | 4067 | 2.6 |
| 10M | M = 8; efConstruct = 100 | 3440 | 2.0 |
| 100M | M = 16; efConstruct = 40 | 40011 | 26 |
查询性能
查询性能主要是看召回率和耗时的关系。在 HNSW 算法中,增大参数 efSearch 可以提高结果的召回率,同时也会增加查询耗时。在下面的结果曲线中,横轴为召回率,纵轴为查询耗时,如果要对比不同算法,则曲线越靠近右下角表示算法效果越好。这里的结果都是单线程查询时的结果。
数据集 10M; M = 16; efConstruct = 500
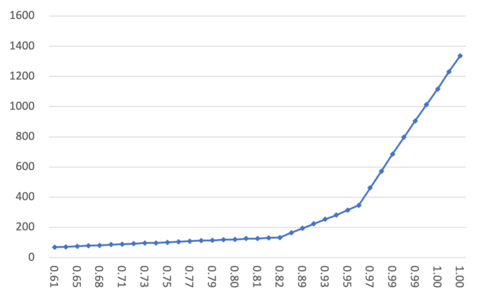
数据集 10M; M = 16; efConstruct = 100
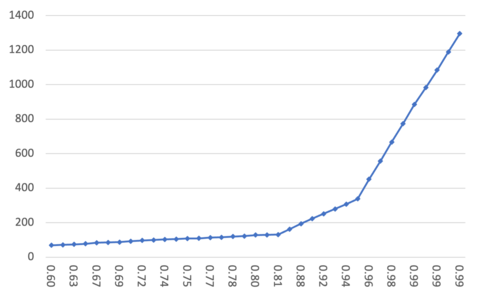
数据集 10M; M = 8; efConstruct = 100
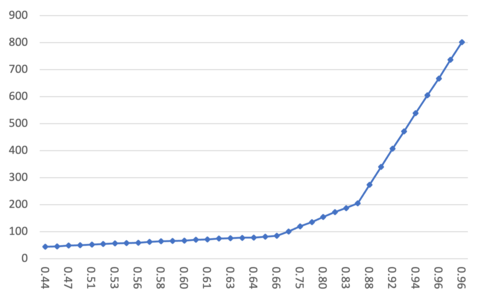
数据集 100M; M = 16; efConstruct = 40